A number is factored in using prime numbers, or primes, in the process known as prime factorization. The explanation of all the prime factorization principles and techniques in this article will assist the students in learning how to quickly identify a number’s prime factors.
The simplest method for determining a number’s prime factors is to keep dividing the starting number by prime factors until the result equals 1. When we divide the number 30 by its prime factors, we obtain 30/2 = 15, 15/3 = 5, and 5/5 = 1. We received the balance, thus it cannot be factored any further. In light of the fact that 2, 3, and 5 are prime factors, 30 = 2 x 3 x 5.
2, 3, 5, 7, 11, 13, 17, and so forth are the first few prime numbers. When these prime numbers are multiplied by any natural integer, composite numbers are created.
Let’s talk about what prime factorization is and how to get its prime factors using various techniques and examples.
Finding a number’s prime factors in a way that the original number may be divided equally by them is known as prime factorization. Since a composite number might have more than two factors, this method can only be used with composite numbers rather than prime numbers.
For instance, since 2 3 3 7 = 126 and 2, 3, and 7 are prime numbers, the prime factors of 126 will be 2, 3, and 7.
Prime factorization Examples:
- Prime factorization of 12 is 2 × 2 × 3 = 22 × 3
- Prime factorization of 18 is 2 × 3 × 3 = 2 × 32
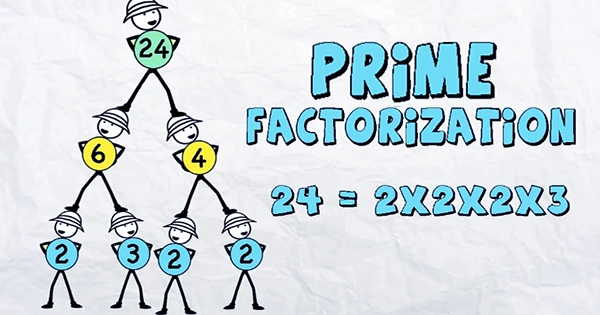
- Prime factorization of 24 is 2 × 2 × 2 × 3 = 23 × 3
- Prime factorization of 20 is 2 × 2 × 5 = 22 × 5
- Prime factorization of 36 is 2 × 2 × 3 × 3 = 2² × 3²